par défaut dans GUM_MC, valeur modifiablePrincipe de la méthode de Monte Carlo ("MCM")
Pour chacune des grandeurs d'entrée, on génére un échantillon
de M valeurs (
par défaut dans GUM_MC, valeur modifiable
dans le menu "options") selon la fonction de densité de probabilité choisie
par l'utilisateur.
On a donc des échantillons:
pour
:
(
,
,...,
)
pour
:
(
,
,...,
)
...
pour
:
(
,
,...,
)
On calcule alors les M valeurs de l'échantillon de sortie:
L'estimateur de sortie est
alors la moyenne
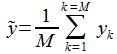
L'estimateur de
l'incertitude-type de sortie est l'écart-type:
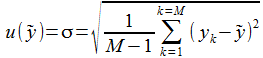
On peut reconstituer la loi de
distribution de Y :
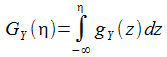
et la PFD de Y,
peut
être tracée sous forme d'histogramme
(le nombre de "classes" est réglable dans le menu "options").
Le coefficient de
dissymétrie ou skewness est estimé par:
.
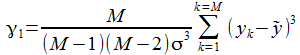Il traduit l'éventuelle dissymétrie de la distribution par rapport à sa moyenne. Il vaut 0 pour une distribution symétrique.
L'excés d'aplatissement ou kurtosis normalisé est estimé par:
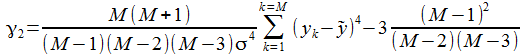
Il vaut 0 pour une distribution normale, -1.2 pour une distribution uniforme.