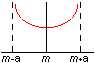
La loi dérivée d'arc sinus est complètement définie à partir de sa moyenne et de son écart type. Si on ne connaît pas la valeur de l'écart type, il est possible de la déterminer à partir de la plage de variation de la variable.

Cas ou l'écart type n'est pas connu

  Connaissant un intervalle englobant toutes les valeurs de la grandeur, si a est la valeur de ce demi-intervalle, alors l'incertitude type est :
  
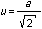
Cette formule est démontrée dans le dossier métrologie n° 22 du site MetGen. Elle est également employée dans l'exemple H1 (§H1.3.4) du GUM [1].

Cas usuel :

température d'un laboratoire climatisé

  Si les variations de la température provoquent une variation de la température dans l'intervalle [t₀ – a ; t₀ + a], alors l'incertitude type vaut :
  

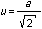
Référence
[1] : JCGM, « Évaluation des données de mesure - Guide pour l'expression de l'incertitude de mesure », BIPM, JCGM 100:2008 (version française), septembre 2008, www.bipm.org.