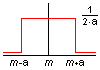
La loi rectangle est complètement définie à partir de sa moyenne et de son écart type. Cette loi doit être employée lorsque que l'on sait que toutes les valeurs sont équiprobables sur un intervalle donné. Si on ne connaît pas la valeur de l'écart type, il est possible de la déterminer à partir de la plage de variation de la variable.

Cas ou l'écart type n'est pas connu

  Connaissant un intervalle englobant toutes les valeurs de la grandeur, si a est la valeur de ce demi-intervalle, alors l'incertitude type est :
  
Cette formule correspond à l'équation (7) du GUM [1].

Cas usuels :

résolution d'un indicateur numérique

Si la résolution est r, alors l'incertitude type vaut :
  

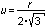
hystérésis

Si la différence maximale obtenue entre les indications obtenues par valeurs croissantes et décroissantes est δ, alors l'incertitude type vaut :
  

instrument vérifié et conforme à une classe d'exactitude

si ± e est l'erreur maximale tolérée, alors l'incertitude type vaut :
  

Exemples :

1) On dispose d'un thermomètre de résolution 0,1 °C. La demi-étendue est a = 0,05 °C et l'écart type 0,05 / √3 °C.

2) On dispose d'un bain thermostaté muni d'un thermomètre étalon. D'après le rapport de caractérisation du bain, la température en un point quelconque du volume de travail diffère de ± 0,02 °C de la tempéraure mesurée par le thermomètre étalon en raison de l'inhomogénéité du bain. L'incertitude due à l'inhomogénéité se calcule en considérant une demi-étendue a valant 0,01 °C et donc un écart type valant 0,01 / √3 °C.

Référence
[1] : JCGM, « Évaluation des données de mesure - Guide pour l'expression de l'incertitude de mesure », BIPM, JCGM 100:2008 (version française), septembre 2008, www.bipm.org.