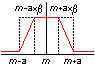Choix d'une loi
Le choix d'une distribution se fait en utilisant le principe du maximum d'entropie. Ce principe hérité de la théorie de
l'information signifie qu'on utilise toute l'information disponible sans ajouter d'hypothèses. Par exemple si on sait
qu'une variable varie entre deux valeurs on choisira une distribution rectangulaire. Si on sait en plus que la valeur centrale
est plus probable, on choisira alors une distribution triangulaire.
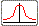
1. Loi Normale
| Distribution |
Utilisation |
|
|
 répétabilté d'une mesure ; répétabilté d'une mesure ;
 correction donnée par un certificat d'étalonnage. correction donnée par un certificat d'étalonnage.
Si la seule information disponible est une moyenne et un écart type alors cette loi doit
être retenue :
la distribution normale présente l'entropie maximale parmi toutes les lois ayant
une même moyenne et un même écart type.
|
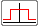
2. Loi rectangle
| Distribution |
Utilisation |
|
|
 résolution d'un indicateur numérique ; résolution d'un indicateur numérique ;
 hystérésis hystérésis
 instrument vérifié, conforme à une classe d'exactitude instrument vérifié, conforme à une classe d'exactitude
 homogénéité d'un milieu de comparaison homogénéité d'un milieu de comparaison
 stabilité d'un moyen de comparaison. stabilité d'un moyen de comparaison.
Cette loi doit être retenue lorsque l'on sait simplement que la valeur est comprise entre
une borne inférieure et une borne supérieure ou que l'on sait que toutes les valeurs sont
équiprobables.
|
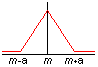
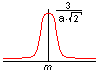
3. Loi triangle
| Distribution |
Utilisation |
|
|
La loi triangle est à utiliser lorsqu'une valeur est contenue dans un intervalle et dont on sait que la valeur centrale est la plus probable.
|
4. Loi trapèze
| Distribution |
Utilisation |
|
|
La loi rectangle suppose que toutes les valeurs sont contenues strictement dans un intervalle.
Ce cas de figure s'applique à une résolution.
En revanche pour une grandeur physique, il y a rarement une rupture brutale mais une décroissance.
Dans ce cas une loi trapèze reflète mieux la réalité.
|
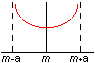
5. Loi dérivée d'arc sinus
| Distribution |
Utilisation |
|
|
Effet de grandeurs d'influence évoluant de façon supposée sinusoidale (par exemple température d'un local climatisé).
|












 répétabilté d'une mesure ;
répétabilté d'une mesure ; correction donnée par un certificat d'étalonnage.
correction donnée par un certificat d'étalonnage.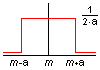
 résolution d'un indicateur numérique ;
résolution d'un indicateur numérique ; hystérésis
hystérésis  instrument vérifié, conforme à une classe d'exactitude
instrument vérifié, conforme à une classe d'exactitude  homogénéité d'un milieu de comparaison
homogénéité d'un milieu de comparaison  stabilité d'un moyen de comparaison.
stabilité d'un moyen de comparaison.